SPSS 졸업논문 판별타당성 개념 및 분석 방법

카테고리 없음

by 통계친구 2019. 6. 30. 20:34

바로 어제 포스팅에 "타당성(Validity)"에 대한 내용을 설명하였다.

다시 한 번 타당성을 짚고 넘어가면, 타당성이란 "제대로 질문한 것이 맞는가?"에 대한 것이다.

1. 판별타당성(Discriminant Validity) 개념
타당성 중에서 판별 타당성은 내 연구에 쓰이는 여러 변수들이 정말로 그 숫자만큼 독립적인 존재로 구별되는지 보는 것이다.
쉬운 설명을 위해 다중회귀분석으로 예시를 들었다.(***다중회귀분석에 대해서는 다음 포스팅에서 설명해주겠다 + 단순회귀분석도 함께)
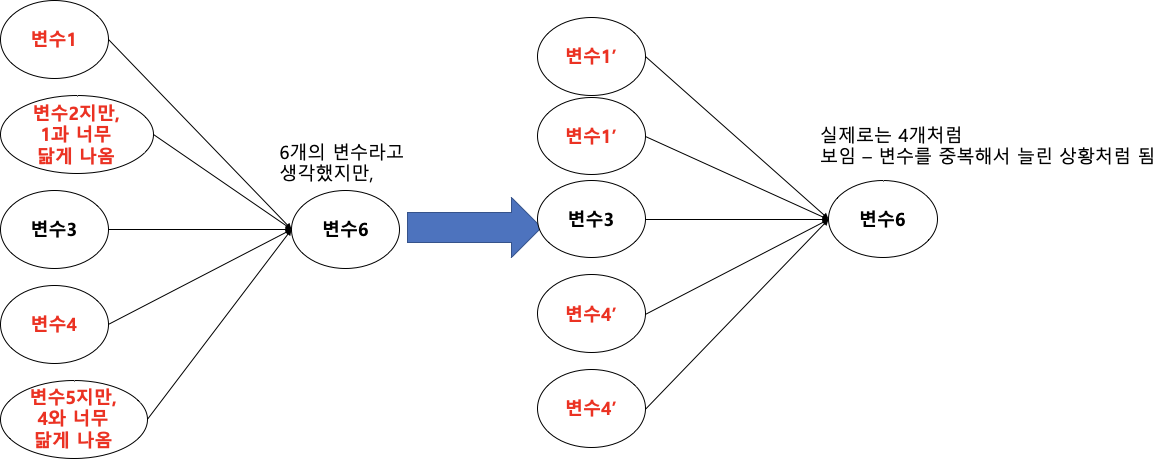
이 예시에는 선행연구를 참고하여 6개의 변수로 가설을 세우고 연구모형을 만들었다. = <그림 1>
원래는 <그림 1>처럼 6개의 변수가 존재한다고 판별(=구별)되어야 정상이다. 즉, 제대로 설문조사를 한 셈이다.
만약, 측정문항이 잘못 되었거나, 설문 응답자가 대충 대답했을 경우 <그림 2>처럼 잘못된 결과가 발생한다. = 5개 이하로 변수 존재

<그림 1> 정상적으로 변수를 측정했을 때 결과 = 6개의 변수 존재

<그림 2> 판별타당성에 문제가 있을 때 예시 = 6개가 안 됨...ㅠㅠ

2. 판별타당성에 문제가 발생하면 뭐가 안 좋은가?

굳이 왜?? 똑같은 변수를 중복해서 넣었냐?? 이런 중복 행위가 뭔 의미가 있냐? 라고 공격 받는다.
즉, <그림 3>과 같은 상황과 같다. 굳이 왜?? 똑같은거 2번 이상 넣냐? 뭐가 이상하다. 제대로 연구한거 맞냐? 는 교수님들의 공격을 받는다.
상식적으로 이런 결과를 보면 뭔가 잘못된 것이 있다고 판단될 것이다.

판별타당성의 문제로 인해 발생하는 최종적인 문제
= 회귀분석 결과에 왜곡된 결과를 일으킨다.
= 회귀계수가 왜곡된다.
= 논문의 결과가 이상해진다.
= 연구 다시 해야 한다.
= 졸업이 늦어진다.
= 대학원 그만 다니고 싶은 마음이 든다.

***물론 더 큰 상위 개념의 변수로 묶어 분석을 계속 진행할 수도 있다. 하지만! 일단, 우리는 변수들을 섬세하게 하나하나 구분하고 싶고, 섬세하게 나누어지는 판별(=구별) 결과를 원한다는 가정을 둔다.

<그림 3> 판별타당성 문제가 있는 경우

판별타당성에 문제가 있으면 즉 다중공선성이 있다고 판단할 수 있다.

2-1. 다중공선성 개념
독립변수들 간 양(+), 음(-)의 상관관계가 너무 높게 나타나 다중회귀분석의 결과를 왜곡시키는 것을 의미한다.
즉, 독립변수들 간의 상호의존도가 높아서 회귀계수의 부호가 양(+)에서 음(-)으로 왜곡되거나, 0(영향력 없음)으로 나타나게 한다.

3. 판별타당성 분석 기준

VIF(Variance Inflation Factor) : 5이하(책에 따라 10 이하로 보기도 함)
VIF는 독립변수끼리 서로 독립, 종속이 되어 얼마나 설명이 되는가를 보는 것인데, 설명이 안 될수록 서로 독립적이라 본다.
즉, 독립변수들끼리 서로 설명이 안될수록 다중공선성 문제는 없다.
상식적으로 설명이 안 될수록 서로 상관이 그만큼 낮다는 의미이다.
반대로 독립변수들끼리 상관이 높으면 서로 설명하는 정도가 높게 나타날 것이다.
공차 0.2 이상
VIF나 공차 중 아무거나 보면 된다.(이유는 VIF의 역수가 공차이기 때문)
그러나 대부분의 논문에서 VIF값을 적는다.

4. SPSS 판별타당성 분석 방법

1) 분석 -> 회귀분석 -> 선형 클릭
분석을 누른 후, 회귀분석을 누른 후, 선형을 누른다.

<그림 4> SPSS 판별타당성 분석 과정 1

2) 독립변수들을 오른쪽에 독립변수 칸에 옮김 -> 종속변수를 오른쪽 종속변수 칸에 옮긴다.

<그림 5> SPSS 판별타당성 분석 과정 2

3) 통계량 설정 -> 공선성 진단 클릭 -> 계속 -> 확인
***사실 이 과정은 다중회귀분석 과정이다. 그러나 판별타당성을 중심적으로 설명을 하는 것이니, 다른 옵션에 대한 설명은 생략한다.

<그림 6> SPSS 판별타당성 분석 과정 3

4) 판별타당성 분석 결과 해석
이 결과는 다중회귀분석에 초점을 맞춘 포스팅이 아니다.
그러니 표준화 계수 베타, t, 유의확률에 대한 것 보다는 VIF값에 초점을 두고 설명하겠다.

분석 결과, VIF값은 모두 5이하의 값으로 나타나 다중공선성 문제는 없는 것으로 나타났다.
= 독립변수들은 5개 모두 서로 독립적인 것으로 판단할 수 있다.

<그림 7> SPSS 판별타당성 분석 결과

5) 구조방정식에서는...
판별타당성을 VIF값도 중요하지만 상관관계 표에서 AVE(Average Variance Extracted 평균분산팽창) 값의 제곱근 값을 취한 값이 다른 변수들과의 상관계수보다 높게 나타나는지를 본다. 이 AVE값의 제곱근 값이 다른 변수들과의 상관계수보다 높게 나타나면 변수들은 판별(=구별) 가능하다고 보고, 판별타당성에 문제가 업다고 본다.

<그림 7> AMOS 판별타당성 분석 결과 예시